Sabemos que todos los números enteros es posible expresarlos como el producto de potencias de números primos. A esto es a lo que se le llama descomposición de un número en sus factores primos.
El siguiente código lo encontré entre mis bodegas de cosas , hace tiempo que no lo veía, es bastante interesante y simple de programar. No recuerdo bien cual fué la razón por la que lo programe, pero parece que alguien me lo pidió como favor creo.. en fin, la idea es simple dada una entrada de un entero representar su descomposición en números primos.
Este método es realmente eficaz para descomponer cualquier número en sus factores primos. Puedes averiguar como funciona siguiendo tú mismo el código que está a continuación…
Asi que si justo tienes un tiempo de descanso entre tus innumerables preguntas matemáticas , preguntándote si algún día vas a fabricar algún programa que te permita encontrar los factores primos de un número, entonces estás de suerte.
Espero que este código les pueda ayudar en algo, si tienen dudas, solo dejen un comentarios.
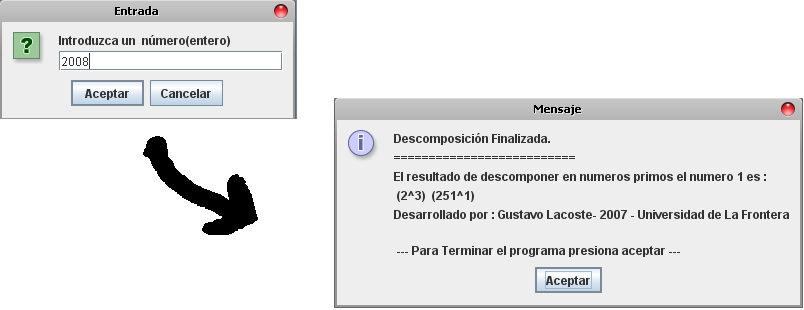
Código DescompNumPrimos.java
package descomponernumeroenfactprimosenformavoraz;
import java.io.*;
import java.lang.Math;
import javax.swing.*;
public class DescompNumPrimos {
/**
* Él siguiente método es el constructor de la clase , lo que realmente hace
*es
*/
public DescompNumPrimos() {
JOptionPane.showMessageDialog(null,»Bienvenido al Programa\n»+
«=======================\n\n»+
«Desarrollado por : Gustavo Lacoste- 2007 – Universidad de La Frontera\n\n» +
«El siguiente programa utiliza la estrategia voraz para descomponer\n» +
«un número N en sus factores primos.\n\n» +
«ADVERTENCIA\n» +
«===========\n» +
«1.- Recuerda que la descomposición NO se puede realizar con números negativos\n» +
«2.- La complejidad del algoritmo es O(n*log2 n)\n» +
«\n — Para continuar presiona aceptar —«);
int numero=this.leerNumero();
descomponerEnFactorPrimo(numero); //Llama al método con el número deseado.
}
/**
* Método para leer un entero por teclado.
* @return Retorna un entero que ha pulsado el usuario.
*/
private int leerNumero() {
try {
return Integer.parseInt(JOptionPane.showInputDialog(null,»Introduzca un número(entero)»));
}
catch (Exception e) {
JOptionPane.showMessageDialog(null,»Error el formato del número introducido es incorrecto, ingresa un entero !!!.»);
return leerNumero(); //esto es recursividad
}
}
/**
* El siguiente método es el que hace casi todo el trabajo, toma un número y realiza la descomposición
*en factores primos de dicho número.
*
*/
public void descomponerEnFactorPrimo(int numeroADescomponer) {
int factorPrimo = 2;
int contadorDeNumeroDeVecesQueApareceCadaFactor;
String flujoDeSalida=»»;
System.out.print(numeroADescomponer + » = «);
while (numeroADescomponer > 1){
contadorDeNumeroDeVecesQueApareceCadaFactor = 0;
while ( (numeroADescomponer % factorPrimo) == 0) {
//encotrado factor
++contadorDeNumeroDeVecesQueApareceCadaFactor;
numeroADescomponer /= factorPrimo;
}
if (contadorDeNumeroDeVecesQueApareceCadaFactor > 0) {
flujoDeSalida=flujoDeSalida+» «+ («(» + factorPrimo + «^» + (contadorDeNumeroDeVecesQueApareceCadaFactor) + «) «);
}
++factorPrimo;
}
JOptionPane.showMessageDialog(null,»Descomposición Finalizada.\n»+
«==========================\n» +
«El resultado de descomponer en numeros primos el numero «+numeroADescomponer+» es :\n» +
flujoDeSalida+»\n» +
«Desarrollado por : Gustavo Lacoste- 2007 – Universidad de La Frontera» +
«\n\n — Para Terminar el programa presiona aceptar —«);
}
/**
* Método main de la clase Problema3, en este método creo el objeto
* de la clase Problema3 el cual automaticamente llamará a su constructor.
*/
public static void main(String[] args) {
DescompNumPrimos instanciaDePrueba = new DescompNumPrimos();
} // Fin del main.
} // Fin de la clase.
Adicionalmente para los fanáticos de los números primos les dejo el enlace a un articulo bastante bueno sobre varias conjeturas de los mismos.
Link
ue se celebra en los días en que tanto el día del mes y el numero del mes son la raíz cuadrada de los dos últimos dígitos del año.
